Sortieren

Einleitung

In der Informatik ist das Sortieren von Daten eine wichtige Aufgabe. Es gibt viele verschiedene Algorithmen, die verwendet werden können, um Daten zu sortieren, und jeder hat seine eigenen Stärken und Schwächen. In diesem Kapitel werden wir uns einige der gängigsten Sortieralgorithmen ansehen und ihre Anwendungen sowie ihre Vor- und Nachteile untersuchen. Wir werden auch sehen, wie man bestimmt, welcher Algorithmus für eine bestimmte Aufgabe am besten geeignet ist und wie man ihn implementiert.

Sortierverfahren

Algorithmen, um Daten anhand eines Kriteriums zu ordnen
Algorithmen unterschiedlicher Komplexität

Eingabe: Unsortierte Daten
Ausgabe: Daten, die anhand des Sortierkriteriums sortiert sind

Ein Verfahren heißt stabil, wenn es die relative Reihenfolge gleicher Schlüssel in den Daten beibehält.

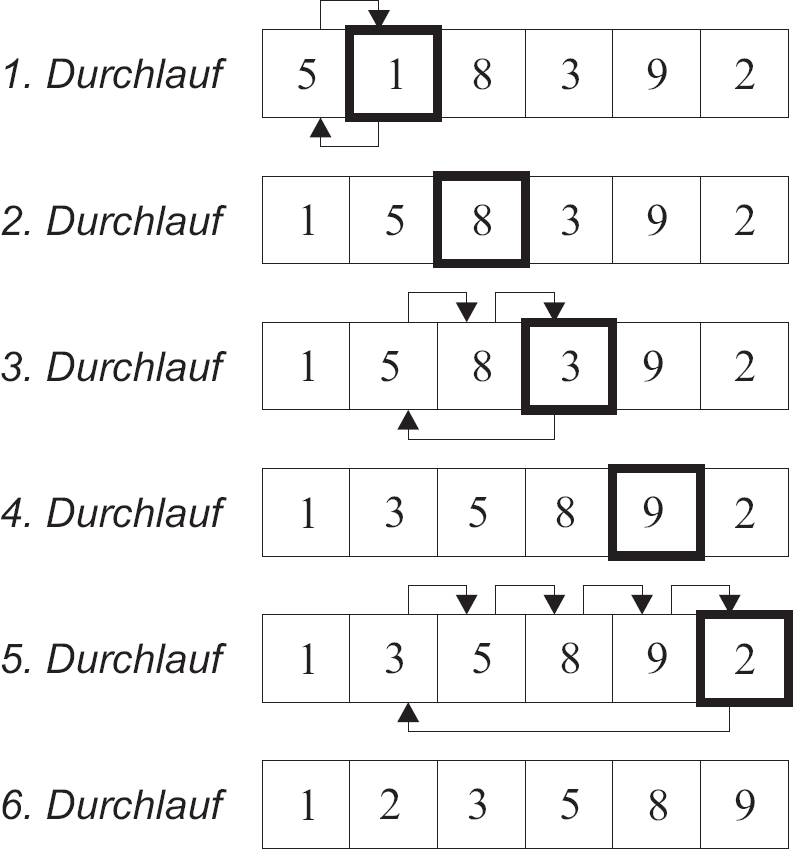
Insertionsort

Insertionsort ist ein einfacher, stabiler Sortieralgorithmus, der auf der Idee des Sortierens einer Hand von Karten basiert. Der Algorithmus geht durch eine Liste von Elementen und fügt jedes Element an der richtigen Stelle in die Liste ein. Dies geschieht, indem das aktuelle Element mit jedem Element verglichen wird und es an der richtigen Stelle platziert wird. Dieser Vorgang wiederholt sich für jedes Element in der Liste, bis die gesamte Liste sortiert ist. Insertionsort hat eine Zeitkomplexität von \( \mathcal{O}(n^2) \) im Worst-Case-Szenario, was es für große Datenmengen ungeeignet macht, es eignet sich jedoch für kleine Datenmengen oder bereits teilweise sortierte Daten.

Starte mit der ersten Karte einen neuen Stapel.
Nimm jeweils die nächste Karte des Originalstapels und füge diese an der richtigen Stelle in den neuen Stapel ein.

Insertionsort in Pseudocode

for i := 1 to n do
  m := F[i]; /* zu merkendes Element */
  j := i;
  while j > 1 do
    if F[j - 1] >= m then
      /* Verschiebe F[j - 1] eine Position nach rechts */
      F[j] := F[j - 1];
      j := j - 1
    else
      Verlasse innere Schleife
    fi
  od;
  F[j] := m /* j zeigt auf Einfügeposition */
od

Quelle: Gunter Saake und Kai-Uwe Sattler: Algorithmen und Datenstrukturen, 6. Auflage

Insertionsort in Java

public void sort(int[] data) {
    for (int i = 1; i < data.length; i++) {
        int m = data[i];
        int j = i;
        while (j > 0) {
            if (data[j - 1] >= m) {
                /* Verschiebe data[j - 1] eine Position nach rechts */
                data[j] = data[j - 1];
                j--;
            }
            else {
                break;
            }
        }
        data[j] = m;
    }
}

Selectionsort

Selectionsort ist ein einfacher, in-place Sortieralgorithmus, bei dem das größte Element in einer Liste ausgewählt und an die letzte Stelle platziert wird. Dann wird der Prozess für die restlichen Elemente wiederholt, indem das nächstgrößere Element ausgewählt und an die nächste Stelle platziert wird, und so weiter, bis die Liste vollständig sortiert ist. Der Algorithmus durchläuft die Liste mehrere Male und vergleicht jedes Element mit jedem anderen Element, um das größte Element zu finden und es an die richtige Stelle zu verschieben. Selectionsort hat eine Zeitkomplexität von \( \mathcal{O}(n^2) \) im Worst-Case-Szenario, was es für große Datenmengen ungeeignet macht, es eignet sich jedoch für kleine Datenmengen oder bereits teilweise sortierte Daten.

Suche die größte Karte im Stapel.
Stecke die größte Karte ans Ende des Stapels.
Wiederhole die Schritte für die verbleibenden Karten.

p := n;
while p > 0 do
  g := Index des größten Elementes aus F im Bereich 1 ... p;
  Vertausche Werte von F[p] und F[g];
  p := p - 1
od

Quelle: Gunter Saake und Kai-Uwe Sattler: Algorithmen und Datenstrukturen, 6. Auflage

public void sort(int[] data) {
    int pos = data.length - 1;
    while (pos >= 0) {
        // bestimme größtes Element
        int indexMax = 0;
        for (int i = 0; i <= pos; i++) {
            if (data[i] > data[indexMax]) {
                indexMax = i;
            }
        }
        // tausche array[pos] mit diesem Element
        swap(data, pos, indexMax);
        pos--;
    }
}

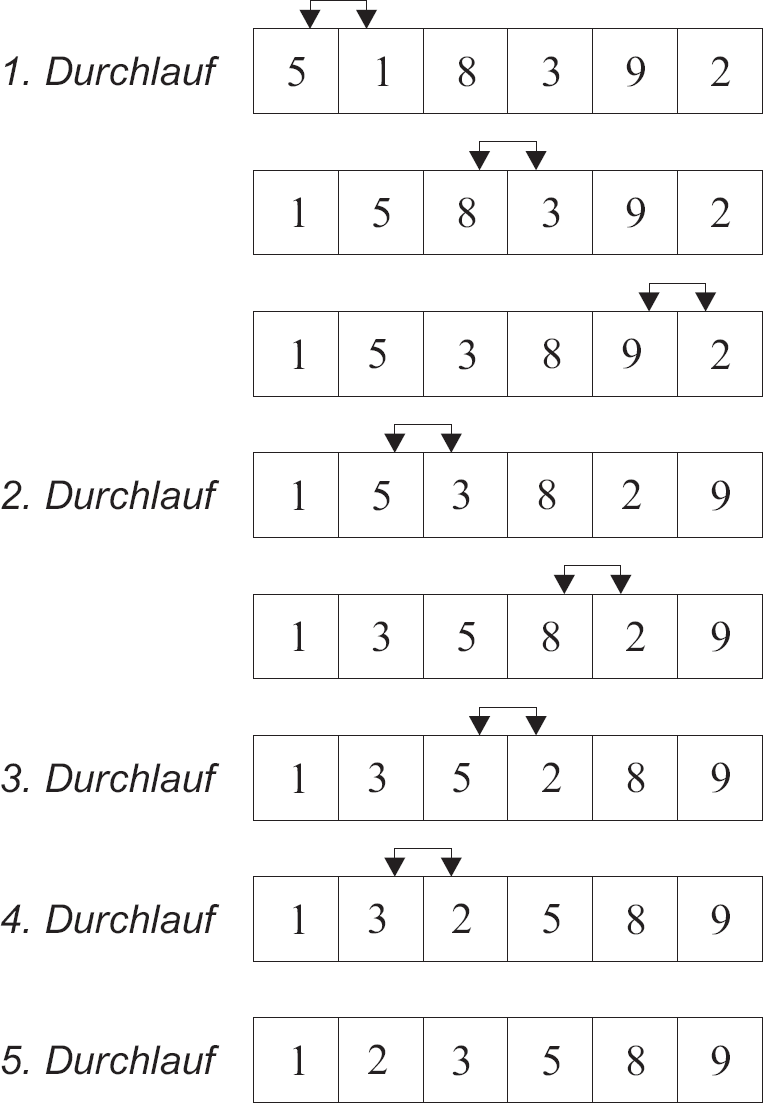
Bubblesort

Bubblesort ist ein einfacher, aber ineffizienter Sortieralgorithmus. Der Algorithmus geht durch eine Liste von Elementen und vergleicht jedes Element mit seinem Nachbar. Wenn ein Element größer ist als sein Nachbar, werden die beiden Elemente vertauscht. Dieser Vorgang wird wiederholt, bis keine weiteren Vertauschungen mehr notwendig sind, was bedeutet, dass die Liste sortiert ist. Bubblesort hat eine Zeitkomplexität von \( \mathcal{O}(n^2) \) im Worst-Case-Szenario und \( \mathcal{O}(n) \) im best case, was es für große Datenmengen ungeeignet macht.

Durchlaufe die Liste und vergleiche die Karte mit dem rechten Nachbarn.
Wenn der rechte Nachbar kleiner ist, vertausche die Karten.
Wiederhole die Schritte, bis keine Vertauschung mehr auftritt.

do
  for i := 1 to n - 1 do
    if F[i]> F[i + 1] then
      Vertausche Werte von F[i] und F[i + 1]
    fi
  od
until keine Vertauschung mehr aufgetreten

Quelle: Gunter Saake und Kai-Uwe Sattler: Algorithmen und Datenstrukturen, 6. Auflage

public void sort(int[] data) {
    boolean swapped;
    do {
        swapped = false;
        for (int i = 0; i < data.length - 1; i++) {
            if (data[i] > data[i + 1]) {
                // Elemente vertauschen
                swap(data, i, i + 1);
                swapped = true;
            }
        }
    } while (swapped);
}

Mergesort

Mergesort ist ein effizienter, stabiler Sortieralgorithmus, der auf dem Prinzip des „Teilen und Herrschens“ basiert. Der Algorithmus teilt die Liste in zwei gleich große Teile und sortiert jeden Teil rekursiv. Sobald beide Teile sortiert sind, werden sie zusammengefügt (merge), indem die Elemente aus beiden Teilen verglichen und in eine neue sortierte Liste eingefügt werden. Dieser Vorgang wiederholt sich, bis die gesamte Liste sortiert ist. Mergesort hat eine Zeitkomplexität von \( \mathcal{O}(n \log{n}) \) im Worst-Case-Szenario, was es zu einem sehr effizienten Algorithmus für große Datenmengen macht. Es benötigt jedoch zusätzlichen Speicherplatz, um die zwischengespeicherten Teillisten zu halten.

Halbiere den Kartenstapel rekursiv in kleinere Teillisten (z. B. 1, 2 oder drei Karten).
Sortiere die Teillisten einzeln
(bei einem Element pro Liste entfällt dieser Schritt).
Füge die Teillisten wieder schrittweise zusammen.

Vergleiche die ersten Elemente der Teillisten und übernimm das kleinere.
Entferne das Element aus der Teilliste und wiederhole den Vergleich.

Quelle: Gunter Saake und Kai-Uwe Sattler: Algorithmen und Datenstrukturen, 6. Auflage

void msort(int[] array, int le, int ri, int[] helper) {
    int i, j, k;
    if (ri > le) {
        // zu sortierendes Feld teilen
        int mid = (ri + le) / 2;

        // Teilfelder sortieren
        msort(array, le, mid, helper);
        msort(array, mid + 1, ri, helper);

        // Hilfsfeld aufbauen
        for (k = le; k <= mid; k++) {
          helper[k] = array[k];
        }

        for (k = mid; k < ri; k++)  {
          helper[ri + mid - k] = array[k + 1];
        }

        // Ergebnisse mischen über Hilfsfeld
        i = le; j = ri;
        for (k = le; k <= ri; k++) {
            if (helper[i] < helper[j]) {
                array[k] = helper[i++];
            } else {
                array[k] = helper[j--];
            }
        }
    }
}

public void sort(int[] data) {
    int[] helper = new int[data.length];
    msort(data, 0, data.length - 1, helper);
}

Quicksort

Quicksort ist ein schneller, in-place Sortieralgorithmus, der auf der Idee des „Teilen und Herrschens“ basiert. Der Algorithmus wählt ein Element als Pivot und teilt die Liste in zwei Teile: Elemente, die kleiner als das Pivot-Element sind und Elemente, die größer sind. Dann wendet er sich rekursiv an jeden Teil, um diese Teile sortiert zu machen. Dieser Vorgang wiederholt sich, bis die gesamte Liste sortiert ist. Quicksort hat eine durchschnittliche Zeitkomplexität von \( \mathcal{O}(n \log{n}) \) was es zu einem der schnellsten Sortieralgorithmen für große Datenmengen macht. Es hat jedoch auch eine worst-case-Zeitkomplexität von \( \mathcal{O}(n^2) \), die durch die Wahl des falschen Pivot-Elements verursacht werden kann. Um dies zu vermeiden, kann man diverse Pivot-Auswahl-Methoden verwenden, um die bestmögliche Leistung zu erreichen.

Wähle ein Pivotelement.
Spalte die die Karten in zwei Teillisten:

Kleiner (oder gleich) dem Pivotelement.
Größer (oder gleich) dem Pivotelement.

Wiederhole die Schritte 1. und 2. bis die Teillisten die Länge 1 haben.
Die Gesamtliste ist sortiert.

Quicksort (F, u, o)
Eingabe: eine zu sortierende Folge F,
die untere und obere Grenze u, o

if o > u then
  Bestimme Position p des Pivot-Elementes;
  pn := Zerlege(F, u, o, p);
  Quicksort (F, u, pn - 1);
  Quicksort (F, pn + 1, o)
fi

Zerlege (F, u, o, p) -> pn
Eingabe: zu zerlegende Folge F, untere und obere Grenze u, o,
Position p des Pivot-Elementes
Ausgabe: neue Position pn des Pivot-Elementes

pn := u;
pv := F[p];
Tausche F[p] und F[o]; // Pivot-Element nach rechts
for i := u to o - 1 do
  if F[i] <= pv then
    Tausche F[pn] und F[i];
    pn := pn + 1;
  fi
od
Tausche F[o] und F[pn]; // Pivot-Element zurück
return pn

int partition(int[] array, int u, int o, int p) {
    int pn = u;
    int pv = array[p];
    // Pivot-Element an das Ende verschieben
    swap(array, p, o);
    for (int i = u; i < o; i++) {
        if (array[i] <= pv) {
            swap(array, pn++, i);
        }
    }

    // Pivot-Element an die richtige Position kopieren
    swap(array, o, pn);

    // neue Pivot-Position zurückgeben
    return pn;
}

void qsort(int[] array, int u, int o) {

    // Pivot-Element bestimmen
    int p = (u + o) / 2;
    if (o > u) {
        // Feld zerlegen
        int pn = partition(array, u, o, p);
        // und Partitionen sortieren
        qsort(array, u, pn - 1);
        qsort(array, pn + 1, o);
    }
}

public void sort(int[] data) {
    qsort(data, 0, data.length - 1);
}

Verfahren im Vergleich

Verfahren	Stabilität	Vergleiche (im Mittel)
Selectionsort	instabil	1/2 n²
Insertionsort	stabil	1/4 n²
Bubblesort	stabil	1/2 n²
Mergesort	stabil	n log₂(n)
Quicksort	instabil	2n ln(n)